Over the past couple of months, I participated in axiom.xyz's open-source program. This program is designed to introduce more contributors to open-source projects within the Zero-Knowledge (ZK) space and provide guidance on writing ZK circuits using Axiom's halo2 libraries.
My contribution to this program was the development of an ed25519 (an instance of EdDSA) signature verification circuit in halo2-lib, axiom's library containing basic building blocks for developing zero-knowledge proof circuits in halo2.
In this post, I'll start by briefly explaining digital signatures, elliptic curves, and ECDSA/EdDSA, before diving into the details of my project and the ZK circuits. For an introduction to halo2, check out the halo2 book.
Background
Digital Signatures
Digital signatures play a important role in confirming the authenticity of digital data. Much like their physical counterparts, digital signatures provide assurance that the data has indeed been created by a known sender (identified by a public key) and has not been tampered with.
Imagine Alice wants to send a message to Bob. She decides to include a digital signature with the message to ensure that it remains untampered. Upon receiving the message and the signature, Bob can use Alice's public key to authenticate the signature and confirm that the message is unaltered. The process is visually depicted below:
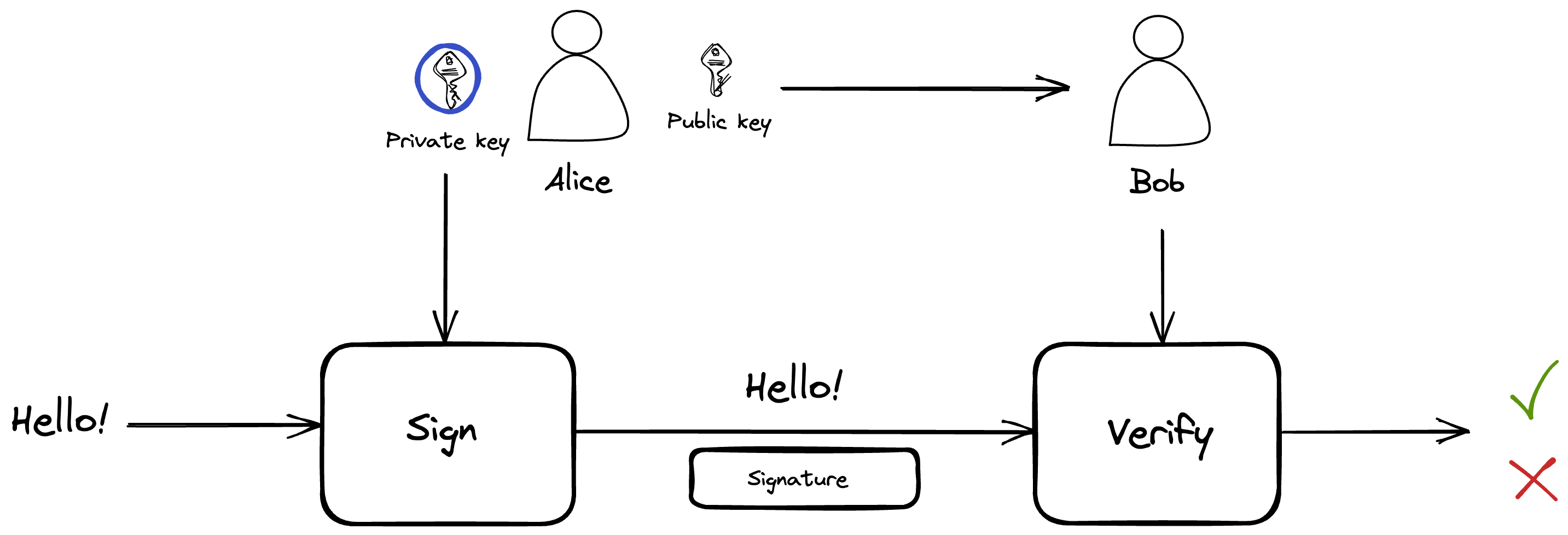
Types of Signature Schemes
Over time, several algorithms have been developed for creating digital signatures, including RSA (based on the hardness of prime factorization), DSA (Digital Signature Algorithm, based on the difficulty of the discrete logarithm problem in prime fields), ECDSA (Elliptic Curve DSA) and EdDSA (which apply the discrete log problem to elliptic curves), and BLS signatures (which are based on more advanced math of elliptic curve pairings).
Our primary focus here is on DSA, which leans on the hardness of the discrete-log problem.
The discrete log problem says that given the above equation for a large prime
ECDSA is essentially DSA applied to elliptic curves. Elliptic curves allow for smaller keys at the same level of security. For example, for 128-bit security - an RSA or DSA signature would require a ~3072-bit key, while an ECDSA or EdDSA signature requires a much smaller ~256-bit key. This results in less computation, leading to faster key creation, encryption, and decryption processes, as well as decreased storage and transmission needs. A great example is in GitHub SSH keys where you'll notice that RSA keys are usually much smaller than their ECDSA/Ed25519 counterparts.
Elliptic Curves
Elliptic curves are these magical mathematical objects that are used in many cryptographic protocols, including ECDSA and EdDSA.
Short Weierstrass Form
Elliptic curves are generally represented in the Short Weierstrass form:
For instance, Secp256k1 which is the curve used for ECDSA in Bitcoin and Ethereum, is represented as
In this form, geometric point addition is defined as follows: given two points on the curve, draw the line connecting these points. Find the third point of intersection of the line with the curve, and reflect this point about the x-axis. The resulting point is the sum of the initial two points. This addition law is visually depicted below:

When this formula is represented algebraically, it leads to six distinct cases based on the various inputs:
Twisted Edwards Form
Twisted Edwards curves follow a different equation:
In these curves, point addition is performed differently: given two points P and Q, draw the rectangular hyperbola that connects these points and the point (0, -1). Find the fourth point of intersection with the curve, and reflect this point about the y-axis. The resulting point is the sum of P and Q. This addition law is shown below:

Although this approach may seem more complex, it has its benefits. Contrary to the Short Weierstrass form that requires six special cases, the Twisted Edwards form has a single formula for all inputs i.e. they have a complete addition law:
A complete addition law does not require handling any exceptional cases. This bring several benefits to cryptographic operations. It simplifies computations, resulting in faster and safer calculations than Weierstrass curves. The simpler and more efficient formulas allow for easier implementation of constant-time operations. This mitigates the risk of timing attacks and bolsters side-channel resistance.
EdDSA
EdDSA or Edwards-curve Digital Signature Algorithm is a variant of the DSA, but is tailored to be faster and more secure than its ECDSA counterpart. EdDSA operates on Edwards curves and eliminates the need for a random nonce, resulting in deterministic signatures. This eliminates risks associated with weak random number generators as a secure source of randomness is no longer necessary.
Sony's PlayStation 3 was famously hacked due to the use of the same nonce across all their ECDSA signatures. EdDSA, by its design, mitigates such risks.
Moreover, it's easier to implement constant time algorithms for Edwards curves, thus making EdDSA more resistant to side-channel attacks like timing attacks. These potential attacks are not theoretical. A recent report showcased a real-world instance of side-channel attack where hackers extracted a 256-bit ECDSA key from a card reader by merely observing the fluctuations of an LED attached to it.
By virtue of its simplicity, EdDSA minimizes room for errors and improves resilience against such side-channel attacks. Also, when verification includes appropriate range checks, EdDSA signatures are non-malleable.
Ed25519
Ed25519, a specific implementation of EdDSA, is described in the RFC8032 standard. The signing and verification algorithms for Ed25519 are summarized below:
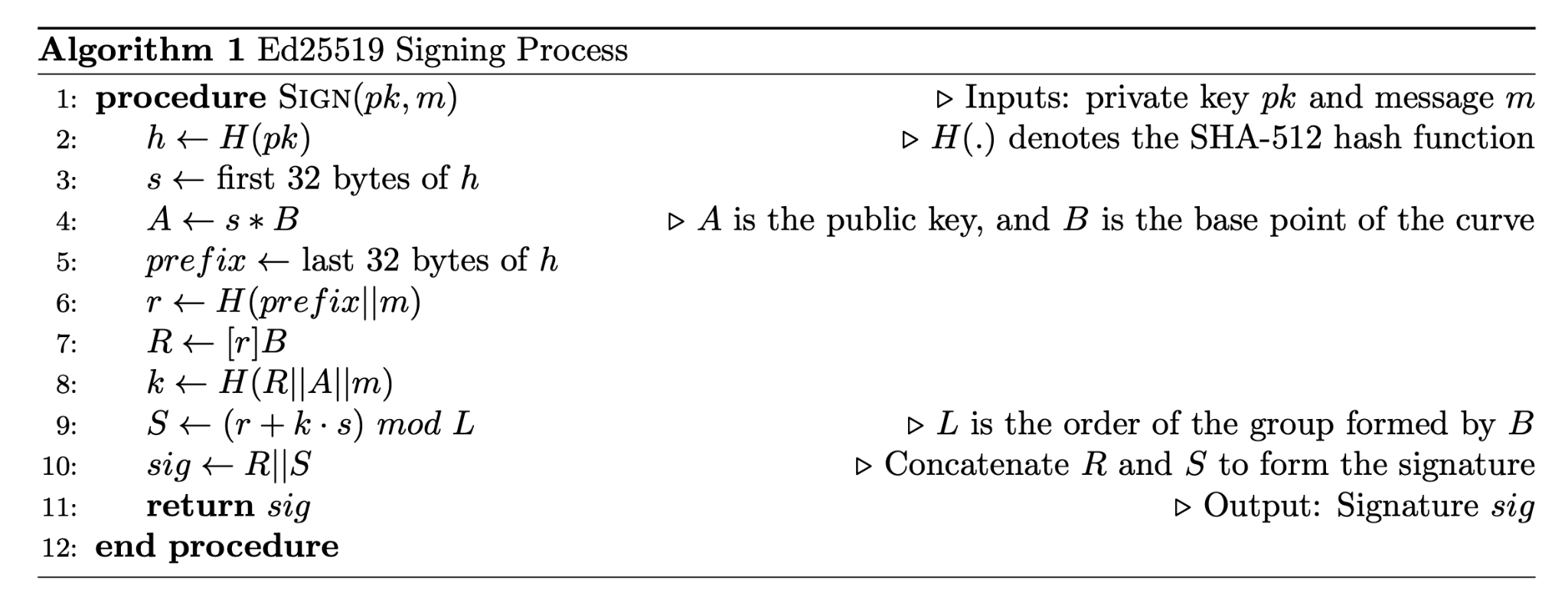

During the verification process, a key detail is that the cofactor of the curve is
EdDSA Verification in ZK
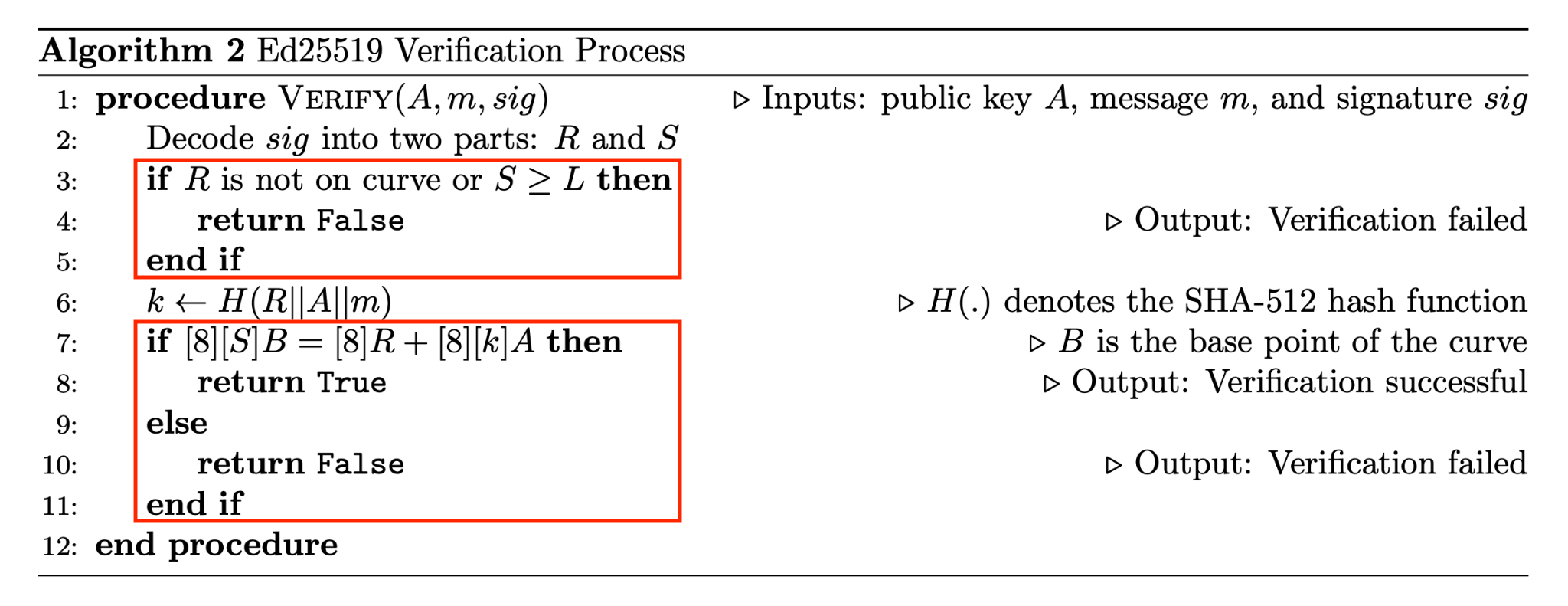
Zero knowledge proofs (ZKPs) provide a mechanism for one party to prove to another that they know a specific piece of information without revealing what that information is. In my project, I implemented the verification of a digital signature scheme within a ZK circuit. The image below illustrates this for a general digital signature scheme. The elements within the red box are implemented inside a ZK circuit.

For Ed25519, the verification algorithm is shown below. All the steps inside the red box were implemented in a halo2 circuit. This involve a few input sanity checks and a final verification equation. To keep the project simple, we didn't do the SHA512 hashing inside the circuit, and instead, it is assumed that the output of the hash k is supplied as an input to the circuit.
Demo
As a practical demonstration, I designed a simple webpage where you can paste a Github commit URL. The page extracts the message and SSH signature from the commit data. If the commit was signed using ed25519, you can query the prover from the page to generate a proof that the signature is indeed valid, and then verify this proof.
A video of the demo is linked below:
My intention was to incorporate the actual demo within this post. However, the prover requires running a server, and I've been unable to get a performant build to run inside the browser using WebAssembly (WASM).
The Circuit
At its core, the verification logic is straightforward. It revolves around the main equation:
An essential detail to remember here is that all these operations take place within an elliptic curve setting. Thus, we have to apply the group addition law of Edwards curves that was discussed earlier.
The aforementioned equation is translated into the following snippet of ZK circuit code, which can be found in eddsa.rs.
// CF is the coordinate field of GA
// SF is the scalar field of GA
#[allow(non_snake_case)]
pub fn eddsa_verify<F: PrimeField, CF: PrimeField, SF: PrimeField, GA>(
chip: &EccChip<F, FpChip<F, CF>>,
ctx: &mut Context<F>,
pubkey: EcPoint<F, <FpChip<F, CF> as FieldChip<F>>::FieldPoint>, // A
R: EcPoint<F, <FpChip<F, CF> as FieldChip<F>>::FieldPoint>,
s: ProperCrtUint<F>,
msghash: ProperCrtUint<F>,
var_window_bits: usize,
fixed_window_bits: usize,
) -> AssignedValue<F>
where
GA: CurveAffineExt<Base = CF, ScalarExt = SF>,
{
let base_chip = chip.field_chip;
let scalar_chip =
FpChip::<F, SF>::new(base_chip.range, base_chip.limb_bits, base_chip.num_limbs);
// Check s < L
scalar_chip.enforce_less_than_p(ctx, s.clone());
// Compute h = H(R || A || M)
let k = msghash;
// Compute sB
let sB = fixed_base::scalar_multiply(
base_chip,
ctx,
&GA::generator(),
s.limbs().to_vec(),
base_chip.limb_bits,
fixed_window_bits,
);
// Compute kA
let kA = scalar_multiply::<F, FpChip<F, CF>, GA>(
base_chip,
ctx,
pubkey,
k.limbs().to_vec(),
base_chip.limb_bits,
var_window_bits,
);
// Compute R' = sB - kA
let R_prime = ec_sub::<F, FpChip<F, CF>, GA>(base_chip, ctx, &sB, &kA);
let sub = ec_sub::<F, FpChip<F, CF>, GA>(base_chip, ctx, &R, &R_prime);
let cofactor = scalar_chip.load_constant(ctx, biguint_to_fe(&(BigUint::from(8u32))));
let sub_mul_cofactor = scalar_multiply::<F, FpChip<F, CF>, GA>(
base_chip,
ctx,
sub,
cofactor.limbs().to_vec(),
base_chip.limb_bits,
var_window_bits,
);
// Check if 8(R - R') = O
base_chip.is_zero(ctx, &sub_mul_cofactor.x)
}The implementation of the ellitpic curve operations in the halo2 circuit is located in the EccChip and covers Edwards curve operations like ec_add, ec_sub and scalar_multiply.
Each term in the Edwards curve formula represents a field element in Curve25519, which differs from the native proving field used in halo2. Therefore, we must implement non-native field arithmetic. To do this, we utilize the FieldChip from halo2-lib and initialize it with implementations of the coordinate field Fp and scalar field Fq of Curve25519. The field chip uses BigInt math from halo2-lib for non-native field arithmetic.
These were my primary contributions in this project.
Circuit Statistics
halo2-lib already has an implementation of ECDSA on Secp256k1, which I used as a benchmark to compare the performance of Ed25519. My implementation of Ed25519 uses more cells than ECDSA (about 3-4 times more).
Here's a quick comparison:
| EdDSA | ECDSA | |
|---|---|---|
| Advice | 1740099 | 513219 |
| Lookup | 317424 | 76475 |
| Fixed | 8025 | 8024 |
The following circuit parameters were used to generate the statistics above:
| Degree | 18 |
| Number of advice columns | 2 |
| Number of lookup columns | 1 |
| Number of fixed columns | 1 |
| Lookup bits | 17 |
| Limb bits | 88 |
| Number of limbs | 3 |
Benchmarks
In terms of raw performance, my implementation of Ed25519 is around 2-3 times slower compared to ECDSA. Here are the performance benchmarks:
| Degree | Num Advice | Num Lookup | Num Fixed | Lookup Bits | Limb Bits | Num Limbs | Proving Time | Proving Time (ECDSA) | Proof Size | Proof Size (ECDSA) | Verification Time | Verification Time (ECDSA) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 19 | 1 | 1 | 1 | 18 | 88 | 3 | 9.94164425s | 8.005132291s | 1920 | 960 | 2.7505ms | 5.328333ms |
| 18 | 2 | 1 | 1 | 17 | 88 | 3 | 8.31224275s | 4.906373625s | 3200 | 1344 | 3.480666ms | 2.286416ms |
| 17 | 4 | 1 | 1 | 16 | 88 | 3 | 6.744536916s | 3.032626125s | 5632 | 1920 | 4.0515ms | 2.503583ms |
| 16 | 8 | 2 | 1 | 15 | 90 | 3 | 6.446831041s | 2.842088166s | 10976 | 3552 | 5.583583ms | 6.247541ms |
| 15 | 17 | 3 | 1 | 14 | 90 | 3 | 7.063340083s | 2.262267208s | 22688 | 6560 | 8.970541ms | 4.175708ms |
| 14 | 34 | 6 | 1 | 13 | 91 | 3 | 7.683013458s | 2.4735815s | 45760 | 12704 | 15.113666ms | 8.189ms |
| 13 | 68 | 12 | 1 | 12 | 88 | 3 | 10.655520208s | 3.070533291s | 93632 | 24960 | 29.344625ms | 10.874083ms |
It's important to remember that my Ed25519 implementation is a proof of concept, and not optimized for performance. I believe there are numerous possible optimizations that could boost performance.
Future Improvements
While the Ed25519 verification works, there are various improvements that can be made to further boost the performance and functionality of the system:
-
Extended Coordinates: Using extended coordinates (x, y, z), as opposed to the currently used affine (x, y) coordinates, would reduce the number of field operations. This should lead to improved overall performance.
-
In-Circuit SHA-512 Hashing: Doing the SHA-512 hashing inside the circuit would remove dependency to external libraries and keep all operations within the circuit.
-
Batch Verification The ability to verify signatures in batches could significantly accelerate processing times, particularly when verifying a large number of signatures.
Conclusion
At the start of this project, I had a basic understanding of halo2 and other modern zero-knowledge proving systems. This journey provided a practical way to better understand these systems. Along the way, my Rust programming skills also improved, even though I occasionally grappled with Rust traits.
Understanding and implementing the elliptic curve based digital signature schemes also taught me the underlying math. I became familiar with the EdDSA signature scheme and the Edwards curve.
In short, this project was an enriching experience that deepened my knowledge and understanding of cryptography. I'm grateful to Axiom for giving me this opportunity.
You can find the code for this project on my GitHub repository.